CAO- Cognitive Adaptive Optimization
Despite the recent advances in the field of control systems, the problem of designing efficient algorithms for practical Large-Scale Networked Control Systems (LSNCS) is all but trivial. This is partly due to the fact that practical control design approaches are often based on simplified models for the LSNCS dynamics and, as a result, the resulting controller parameters may be far from being optimal, or in some cases, even acceptable. This difficulty in conjunction with the intrinsic parametric and dynamic uncertainties of the system characteristics lead to the necessity for major fine-tuning of the originally designed controller parameters. Moreover, medium- or long-term variations of the system dynamics may call for accordingly frequent updates. In the majority of LSNCS the fine-tuning process is performed by experienced personnel based on field observations and by experimenting with different combinations of controller parameters, without the use of a systematic approach. Such a fine-tuning procedure may take months or even years until the control system reaches an acceptable performance.
To deal with the above mentioned shortcomings, we have developed the Cognitive-based Adaptive Optimization (CAO) approach. Its main attributes are summarized as follows:
- According to strict mathematical arguments as well as extensive experiments it guarantees efficient rapid and safe on-line optimization of the operations of general optimization & control systems regardless their scale and complexity and the uncertainty of the environment they are operating on
- Moreover it can be applied to any type of LSNCS regardless of the system’s particular operations and the control elements involved
- It is utterly generic computationally efficient and straightforward to embed in any type of LSNCS regardless of its size level of complexity and level of decentralization
- It incorporates powerful adaptation and estimation mechanisms which render it adaptable and robust to short-term and long-term variations of the LSNCS operations such as e.g. weather and other environmental variations infrastructure modifications etc
- It can straightforwardly incorporate and combine user-imposed constraints and requirements
- Last but not least it rules out the possibility of poor performance while the optimization process is active
The CAO methodology can be briefly described as follows. Consider the problem where a controller of the form:
u=g(K,x)
is applied to the large-scale networked system, where u denotes the vector of control actions to the system, x denote the vector of system’s sensor measurements (which may correspond to measurements of the states of the systems as well as measurements of exogenous factors affecting the system), K denotes the controller gain matrix and g(.) is a possibly nonlinear function. Typically, the nonlinear function g(.) is obtained by employing control system design principles to the controlled system, while an initial value for the controller matrix K can be obtained using either control design principles or simulation-based optimization using a simulation model for the LSNCS. Apparently, this initial value for the controller gain matrix K may be far from its optimal value. Moreover and no matter whether the initial controller gain matrix K is or is not far to its optimal value, the short-, medium- or long-term variations and changes in the LSNCS dynamics call for a continuous update of the controller gain matrix K so as to compensate for these variations and changes.
The CAO approach for continuously updating the controller gain matrix may be summarized as follows:
- The controller u=g(K,x) is applied over some time period. At the end of this period, the CAO system receives the value of the real (measured) performance of the system under the controller u=g(K,x), as well as the values of the most significant external factors affecting the LSNCS dynamics.
- Using the measured quantities, the CAO system calculates new tunable parameter values of the controller gain matrix K to be applied at the next time-period in an attempt to improve the system performance while meeting the user-imposed constraints and requirements.
- This (iterative) procedure is continued over many time-periods until a maximum in performance is reached; then, the on-line optimization procedure remains active for continuous adaptation in order to account for the medium and long-term changes in the LSNCS dynamics.
The details of the CAO algorithm – in its simplest form – are described below.
| Choose a positive integer Initialize the controller parameters Choose a positive function (1) An example of a function |
Step 1. Apply the controller u=g(K,x) over the time-period ![]() and calculate the system performance
and calculate the system performance ![]() for this period.
for this period.
Step 2. Construct a Linear-In–the-Parameters (LIP) approximator ![]() of
of ![]() as follows:
as follows:
(2) ![]()
(3) 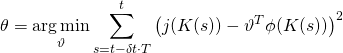
where ![]() being the vector of the approximator’s regressor terms and the vector of the parameters of the approximator and
being the vector of the approximator’s regressor terms and the vector of the parameters of the approximator and ![]() .
.
Step 3. Generate ![]() candidate perturbed version of the matrix
candidate perturbed version of the matrix ![]() as follows:
as follows:
(4) ![]()
where ![]() are random matrices with the same dimensions as the matrix
are random matrices with the same dimensions as the matrix ![]() .
.
Step 4. Update the estimate ![]() to be equal to the candidate perturbed version that optimizes
to be equal to the candidate perturbed version that optimizes ![]() , i.e.,
, i.e.,
(5) ![]()
Set ![]() and GO TO Step 1.
and GO TO Step 1.
It has to be emphasized that the CAO algorithm presented in Table I can be easily modified so as to account for user-imposed or other constraints and requirements or the case where exogenous factors have a significant influence in the LSNCS dynamics:
- There are many different ways to incorporate user-imposed or other constraints and requirements. In the simplest case, the candidate controller matrices
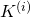 generated in Step 3 are checked whether they meet the constraints and requirements. The ones that do not meet the constraints and requirements are neglected and are not considered in the Step 4 of the algorithm. LIP estimators (similarly to the one of Step 2) can be also employed that estimate/approximate the effect of the candidate controller matrices
generated in Step 3 are checked whether they meet the constraints and requirements. The ones that do not meet the constraints and requirements are neglected and are not considered in the Step 4 of the algorithm. LIP estimators (similarly to the one of Step 2) can be also employed that estimate/approximate the effect of the candidate controller matrices 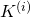 to the constraints/requirements . Alternatively, one may constrain the candidate controller matrices
to the constraints/requirements . Alternatively, one may constrain the candidate controller matrices 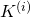 generated in Step 3 by using e.g., constraint projection techniques.
generated in Step 3 by using e.g., constraint projection techniques. - In the cases where exogenous factors have a significant influence in the LSNCS dynamics, the LIP estimator of Step 2 of the algorithm should be augmented so as to be also a function of the exogenous factors. In such a case the estimated performance
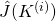 should be also a function of the predicted values of the exogenous factors for the next time-period.
should be also a function of the predicted values of the exogenous factors for the next time-period.

