NDCAO – Neuromorphic Distributed Cognitive Adaptive Optimization

Most modern studies related to artificial intelligence and machine learning domains are strongly driven by advanced statistical recursive algorithms based on artificial neural networks (ANN). Neuromorphic computing and machine-learning has penetrated almost every aspect of our everyday lives stemming from computer vision (object recognition, camera auto-focus, etc.) down to speech recognition, smart-grids and energy management, tactical-army mission management, connected autonomous vehicles, etc.

As the scale of features and complexity of the problem increases the architecture of the ANN might diverge in terms of the number of inputs $x_{i}$ , intermediate hidden layers $K$ , neurons per layer $N_{k}$ , recursive neurons Rk, number of outputs $y_{j}$ . In general, every neuron synapsis imposes two scalar tunable parameters: synapsis weight and bias; which dictate the linear input of the neuron no matter the activation function (logistic sigmoid, hyperbolic tangent, rectifier, soft-plus) selected. As a result, in a generic feed-forwarding complete ANN the number of tunable parameters is proportional to the number of neurons.

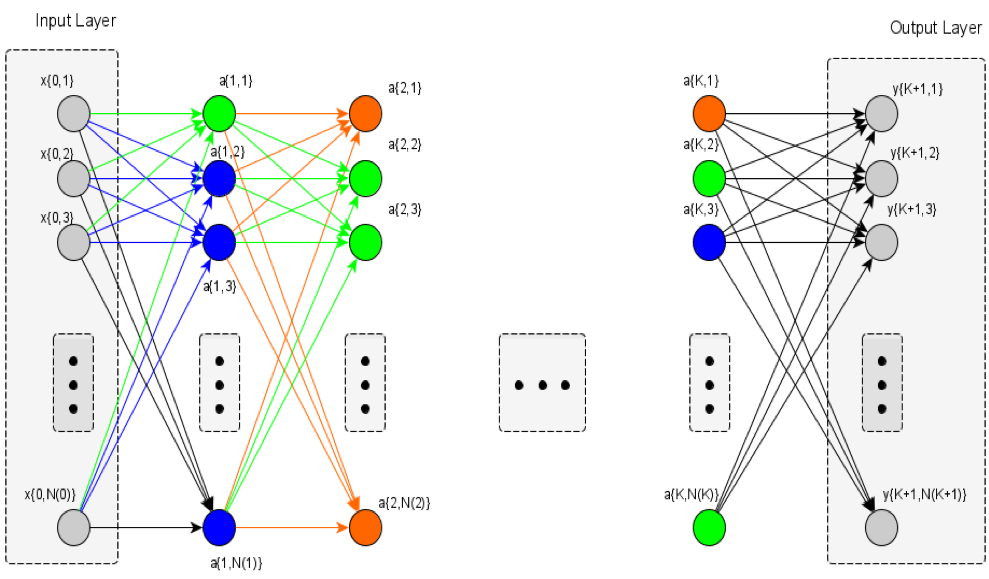
A typical, reliable, accurate yet quite computationally cumbersome supervised learning policy for tuning these parameters is the back propagation, where the error (difference between the ANN actual response and the expected ANN response) of the output layer is the only known error and is propagated back deeper into all the ANN’s layers in order to update each synapsis parameters according to the respective gradient descent rule. More specifically consider the abstract generic feeding-forward ANN as shown in figure below.

The ultimate goal is to calculate and update all $W_{k},B_{k}$ parameters with the ones that minimize an index representing the total divergence/difference of the ANN response, at the final output $(K+1)-th$ layer, with the expected one. As a result, the usual analytic definition of the ANN tuning problem can be formulated as follows:

$min_{W*,B*}J_g(W,B,Y,Y*)$

Where $J_{g}$ is the cost index over a certain set of selected training samples at the ANN output layer, $W$ represents all scalar synaptic weights, $B$ is represents the scalar bias parameters of each synapsis, $Y$ is the set of outputs of the neural network at the edge layer for each respective $X$ training input and ${Y}^*$ are the expected responses of the neural network for each respective $X$ training input.

Several different methodologies/algorithms have gradually emerged in literature trying to resolve this issue through:

Block Coordinate Descent (BCD): where the analytic calculation of the cost function partial derivative (gradient) with respect to each tunable parameter is feasible but convergence might be problematic for intensively non-convex problems.
Centralized Stochastic Gradient Descent (SGD): where the analytic calculation of the cost function gradient with respect to the tunable parameters leads to quite hectic calculations.

Based on the analysis presented in a series of papers published by the ConvCao group, it can be established that the NDCAO, when compared with Centralized Gradient Descent-like and BCD algorithms, possesses the following attributes:

The term ε in the above Table can be sometimes significantly large, which may lead to severe poor performance problems. NDCAO – when compared to BCD – neglects the presence of the term ε, avoiding thus the risk of poor performance.

In order to distribute the cognition load and cope with this centralized learning problem, a plug-n-play, topology-agnostic, scalable learning technique, namely Neuromorphic Distributed Cognitive Adaptive Optimization (NDCAO), has been developed and validated in challenging deep learning problems. NDCAO employs an abstract number of $M\le\sum_{k=1}^{K+1} R_{k}$ locally-driven agents responsible to optimize the response of certain parts of the ANN. The agents are concurrently supervised by a central node in order to synergistically achieve the common objective of minimizing the overall ANN error. NDCAO originates by a thoroughly tested decentralized optimization approach – namely L4GCAO – which has already been evaluated in different simulative and real-life test cases. Leveraging from the L4GCAO paradigm, NDCAO’s algorithmic flow in an online training problem, can be outlined as follows:

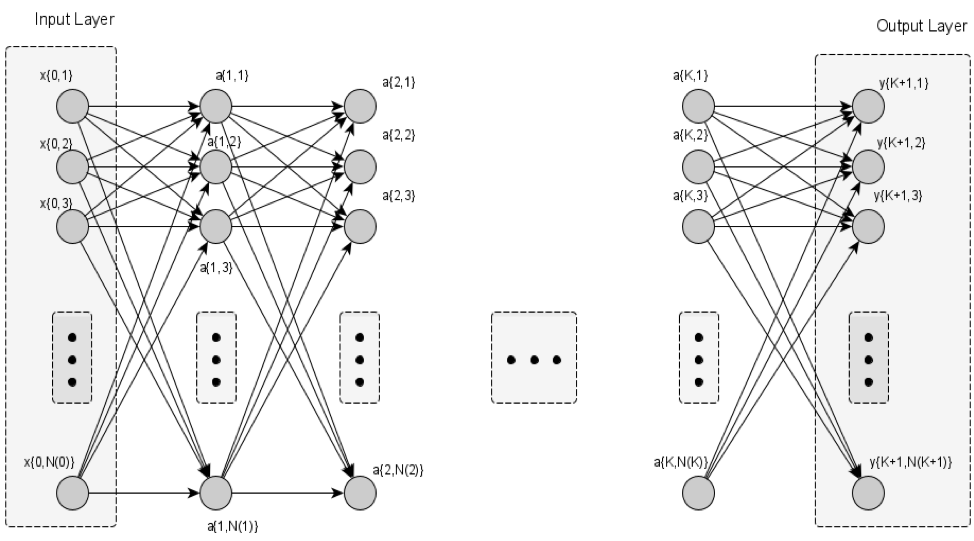
Step-1: Divide the topology of the hidden/intermediate ANN layers, in an abstract or contextual (if feasible) manner, into $M\le\sum_{k=1}^{K+1} R_{k}$ sub-topologies as shown in Figure 2. The topology division does not have to comply with any additional constraint i.e. pooled neurons do not have to necessarily be in the same neighborhood or have a direct interconnection. Let us denote with “ $t$ ” the number of the current training iteration – representing the real-time samples used so far respectively – considered for the ANN training section.

Step-2: Initialize the tunable – i.e. $W_{m},B_{m}$ for linear ANNs – parameters in each constituent/local agent (usually to zeroed values)

$H_{gt}=\begin{bmatrix} H_{10} \\ H_{20} \\ \vdots \\ H_{(M-1,0)} \\ H_{M0} \end{bmatrix} = \begin{bmatrix} W_{m0} \\ B_{m0} \\ \vdots \\ W_{M0} \\ B_{M0} \end{bmatrix}$

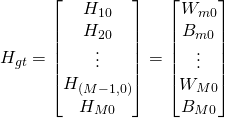
define a reasonable number of training batched-samples interval $T\ge 1$ (depending on the application characteristics and particularities), define a continuous smooth time-decaying positive function representing the random perturbation area size $a(t)$ and define the respective initial value $a(0)\in{R}^+$ .

Step-3: Apply each local set of $H_{mt}$ parameters of the current iteration to each respective autonomous topology of the ANN and by feeding $X_{t}$ in the input $0-th$ layer, calculate the respective response of the ANN $Y_{t}$ at the output-edge $(K+1)-th$ layer.

Step-4: By utilizing the respective $(Y_t,{Y_t}^* )$ values, calculate the overall performance $J_{gt}$ at the end of the current iteration (at the “cloud” central level) and feed each local agent with the respective set of local parameters $H_{mt}$ and the achieved overall performance $J_{gt}$ calculated.

Step-5: At every $``m-th''$ constituent/local agent, calculate, using common least squares techniques, a local linear in the parameters – LIP – estimator of the global objective function $J_{gt}$ ,

Step-6: For every constituent/local agent, generate $P\ge dim\{H_{mt} \} \in \mathbb{N}$ random positive definite perturbations of the pooled ANN local parameters and evaluate them through the respective local estimator resulted from the previous step.

Step-7: For every constituent/local agent, select the set of ANN parameters presenting the most efficient estimated performance for the next timestep, to be applied locally to the system.

Step-8: Go to Step 3 and repeat the process described until performance convergence is reached.

Remark: Note that the feed-forwarding ANN was used only as a more representative application example. Due to its network plant agnostic operational capability, NAMCAO can be easily extended to any type or topology of linear (Mc-Culloch & Pits model or even non-linear Dendritic) ANN without requiring any other tedious preparatory modifications.